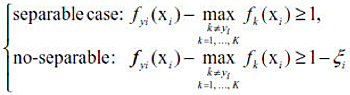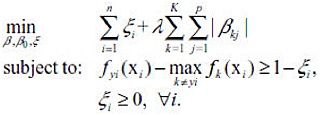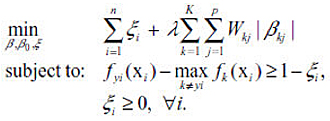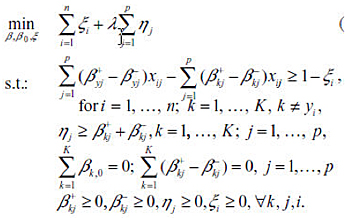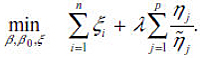Overview
Microarray and RNA-sequencing technologies provide promising tools for cancer diagnosis using gene expression profiles. However, molecular diagnosis based on high-throughput platforms presents great challenges due to the overwhelming number of variables versus the small sample size and the complex nature of multi-type tumors. Support vector machines (SVMs) have shown superior performance in cancer classification due to their ability to handle high dimensional low sample size data. Multiclass support vector machines (MSVMs) provide a natural framework for multi-class learning. Despite its effective performance, the procedure utilizes all variables without selection. Spare MC-SVM (SMS) improves the procedure by imposing shrinkage penalties in learning to enforce solution sparsity. Soft-thresholding type penalties are introduced into the SVM to incorporate variable selection for multi-class classification of high-dimensional gene expression data.
SMS Methods
Given a training set {(xi, yi), i = 1, …, n}, where xi ∈ Rp and yi ∈ {1,2, …, K}, the goal of multiclass classification is to learn the optimal decision rule Φ: Rp → {1,2, …, K} which can accurately predict labels for future observations. For the MSVM, we need to learn multiple discriminant functions f(x) = (f1(x), …, fK(x)), where fk(x) represents the strength of evidence that a sample x belongs to class k. The decision rule is Φ(X) = arg max fk(X) and the classification boundary between any two classes k and l is {x : fk(x) = fl(x)} for k ≠ l.
When K = 2, the label y is coded as {+1, −1} by convention. Consider the linear classifier f(x) = β0 + xTβ. The binary SVM minimizes ||β||2 + λ [sum(ζi)] subject to the following constraint,
SVM:
L1 Penalty (LASSO):
Adaptive L1 Penalty (Adaptive LASSO):
Sup-norm Penalty:
Adaptive Sup-norm Penalty:
The resulting optimization problem has the same constraints as the sup-norm MSVM, with the objective function in Sup-norm replaced with the following:
Reference for Citing
Lingkang Huang, Hao Helen Zhang, Zhao-Bang Zeng and Pierre R. Bushel. Improved Sparse Multi-Class SVM and Its Application for Gene Selection in Cancer Classification. Cancer Informatics, 2013.
Requirements
Matlab ≥ 2006a
Optimization Toolbox
Tomlab
Downloads
Download the Matlab code (250KB) . A Readme file is included to instruct on the execution of the scripts.
Public Domain Notice
This is U.S. government work. Under 17 U.S.C. 105 no copyright is claimed and it may be freely distributed and copied.
Contact
-
Robert P. Bushel, Ph.D.
Special Volunteer -
Tel 919-618-1945
[email protected]