TAGster: Efficient Selection of LD Tag SNP in Single or Multiple Populations
Consider a set S which contains M bi-allelic SNP markers a1,a2...,aM in K populations
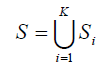
and Si contains Mi SNP markers si1,si2,...,siMi in population i. First, we estimated pairwise LD measure r2 for each SNP pair within each population. Two markers sim and sin are said to be in strong LD if the r2(sim,sin) is greater than or equal to a pre-specified threshold value r0. Both are considered tag SNP for each other, in that sim can be used as a surrogate for sin, or vice versa.
Our aim is to find a tag SNP set, denoted by T, such that for ∀sim ∈Si, i=1,...,K, ∃αj ∈T that satisfies r2(αj,Sim) ≥ r0. In our presentation, we introduce intermediate SNP sets, P and Qi, i = 1,...,K.
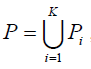
where, Pi is called the candidate set which contains all the SNPs in population i that are eligible to be chosen as a tag SNP, Qi contains SNPs in population i that are already tagged by at least one of tag SNPs in T, i.e. ∀sim ∈Qi, i = 1,...,K, ∃αj ∈T that satisfies r2(αj,Sim) ≥ r0. We implemented several algorithms in TAGster to select tag SNP set T.
Algorithm 1: A greedy algorithm for single or multiple populations
1. Set T = ∅, P1 = S1 and Q1 = ∅, for any 1 =1,...,K;
2. For each SNP αj in P, calculate
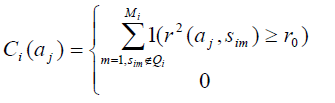
If αj ∈P1
If αj ∉P1
3. Find the SNP αmax that has the highest
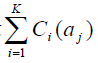
, and add αmax to T. If αmax ∈Pi, add any SNP sim in Pi with r2(αmax, sim) ≥ r0 to Q1 and then exclude αmax from Pi;
4. Repeat Steps 2-3 until Qi=S1 for any 1=1,...,K;
Algorithm 2: An optimal solution for single population tag SNP
An exhaustive Search is performed within each population to find minimal number of population specific tag SNPs Ti for i= 1,...,K.
1. Set Ti = ∅ and Pi=Si, for i=1,...,K;
2. Within population i, partition SNPs in Pi into disjoint precinct Pij, j= 1,...,n, so that r2(sim,sin)<r0 for any two SNPs sim and sin that belong to different precincts.
3. Within a precinct Pij,
- For any two SNPs sim and sin in precinct Pij, if
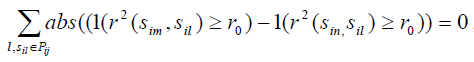
,we exclude one with smaller
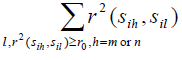
from precinct Pij - Conduct an exhaustive search to find a set of minimum number of tag SNPs for SNPs in precinct Pij and add these tag SNPs into Ti;
4. Repeat step (3) for each precinct
Algorithm 3: Two-stage solution for multi-populations
1. Conduct Algorithm 2 within each population to select a set of population specific tag SNPs Ti for i = 1,...,K;
2. Set T = ∅, Pi = Si for i = 1,...,K;
3. For each SNP tij in Ti, find and SNP sim (sim ∈Pi and sim ∉Ti) that satify r2(tij,Sim) ≥ r0 and then add them as well as tij into LD bin Bij and exclude them for Pi
4. With each LD bin Bij, set Tij = ∅. Find any SNP sim in Bij that satify r2(sim,Sin) ≥ r0 for any SNP sin in Bij, and then add sim to Tij;
5. Set
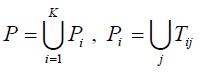
. For each SNP τ in P, l= 1,...,|P|, construct a one dimensional array Al with K elements, where
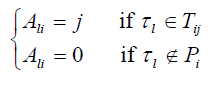
6. Cluster SNPs in P so that any two SNPs τm and τn in a cluster satisfy
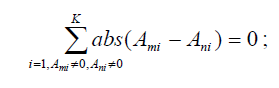
7. Set Ψ = ∅. Find one SNP τl in each cluster with maximum
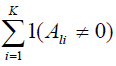
and add it to Ψ.
8. Cluster SNPs in Ψ so that any two SNPs τm and τn in a cluster satisfy
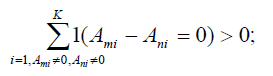
9. For each cluster, set LD bin set B= ∅, record the LD bins in each population that can be tagged by any SNP in the cluster to B, and then conduct an exhaustive search to find a minimum set of tag SNPs in the cluster that can tag all LD bins in B. Add this set of SNPs to T.


